Русскому пенсионеру, да ещё инвалиду первой группы (по старой номенклатуре) только и остается, что раскладывать пасьянс из виртуальных карт, бегать на сверхкороткие дистанции длиной 25 шагов (две комнаты + коридор), пить водку, да разрабатывать никому не нужные идеи и формулы. Например, доказывать, что количество пифагоровых троек так же велико, как количество чисел в натуральном ряду, пифагоровы свойства одного вида пирамид, да разрабатывать технологию затыкания аварийной скважины компании BP, которая четыре месяца возилась с ней, тогда как любой советский боцман мог заткнуть её в два счёта.
Жизнь заставила меня рассчитать скорость движения во льдах одного интересного парохода, который, имея длину не больше 50 м, должен ходить по чистой воде со скоростью 15 узлов и ломать льды. Инженер, да ещё корабел, т.е. специалист высшей квалификации, может сосчитать всё. Ему под силу разработать теорию основ плавания (не движения, а плавания) судов во льдах, да не просто плавания, а ещё и поворачивания, изменить аббревиатуру из русских букв в русском издании на латинскую, применить английские слова в том же издании т.д.
Известно, что лёд (не в холодильнике, а в море) – среда неоднородная, формируется по прихоти природы и не поддаётся строгому описанию. Вообще у каробелов всё ненормально. Они считают качку судов на сумасшедшем море, рассчитывают их прочность, не зная точно, как будет вести себя морская стихия, и пр. Правда жил один учёный (не русский), который захотел узнать с какой скоростью будет идти корабль, хотя бы в идеальной воде, и получил парадоксальный результат, увековеченный его именем. Этот учёный доказал, что какую бы форму корабль не имел, он не будет иметь сопротивление этой самой формы в этой самой идеальной воде.
Примерно также обстоят дела и со льдом. Например, прочность льда на изгиб (основная форма его разрушения судном) может варьироваться в пределах от 300 до 3000 кПа. Поэтому любые расчёты скорости движения судна во льдах имеют условный характер и главное не дают представления о реальной эффективности его работы в этой среде. Но всё-таки хочется сосчитать, и заказчики требуют. Потому договорились рассчитывать так называемую лёдопроходимость (hл), т.е. толщину идеального сплошного ровного льда прочностью 500 кПа без снежного покрова, который может преодолеть судно, двигаясь на минимальной скорости ровным устойчивым ходом. Не строго, но хоть что-то, и позволяет сравнивать различные суда и ледоколы. Ледороходимость определяют сначала в ледовом бассейне. Большие учёные научились моделировать эту непредсказуемую среду, клацая зубами от холода и засеивая поверхность воды концентраторами кристаллообразования. Затем лёдопроходимость со всякими премудростями определяют на естественном полигоне. При этом как ни странно, получают результаты, близкие к модельным. Но в проекте тоже хочется сосчитать эту самую ледопроходимость. Придумано множество многоэтажных формул сложной структуры, иные даже с интегрированием по длине ватерлинии, хотя известно, что линейные интегралы не берутся в чистом виде.
Но один русский учёный – корабел (не специалист по гидромеханике, а сермяжный проектировщик) с корейской фамилией предложил красивую и простую формулу hпр=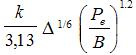
, в которой k – коэффициент, определяемый по прототипу, Pe - тяга всех винтов т, и B - ширина судна по КВЛ в м, 
- водоизмещение в т. Вот в этот прототип всё и уперлось. Судно, о котором сказано выше, имеет более острые обводы, чем все прототипы. Заказчик потребовал выполнить расчёт с учётом этого обстоятельства. В Hanze 97-го года выпуска, № 8 предложена функция, учитывающая влияние формы носовой оконечности на лёдопроходимость - 
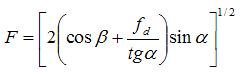, в которой α – угол входа ватерлинии на 1 – 2 теоретических шпангоутах, β - угол развала борта на тех же шпангоутах, fd – коэффициент динамического трения льда о корпус судна (в расчётах в первом приближении 0,1).
После применения этой функции была получена формула hпр=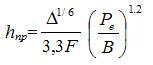
.В ней тяга на винтах измеряется в кН. Коэффициент в знаменателе имеет слабую линейную зависимость от отношения ширины к осадке, но для расчётов можно оставить указанное в формуле значение.
Известно, что лёд (не в холодильнике, а в море) – среда неоднородная, формируется по прихоти природы и не поддаётся строгому описанию. Вообще у каробелов всё ненормально. Они считают качку судов на сумасшедшем море, рассчитывают их прочность, не зная точно, как будет вести себя морская стихия, и пр. Правда жил один учёный (не русский), который захотел узнать с какой скоростью будет идти корабль, хотя бы в идеальной воде, и получил парадоксальный результат, увековеченный его именем. Этот учёный доказал, что какую бы форму корабль не имел, он не будет иметь сопротивление этой самой формы в этой самой идеальной воде.
Примерно также обстоят дела и со льдом. Например, прочность льда на изгиб (основная форма его разрушения судном) может варьироваться в пределах от 300 до 3000 кПа. Поэтому любые расчёты скорости движения судна во льдах имеют условный характер и главное не дают представления о реальной эффективности его работы в этой среде. Но всё-таки хочется сосчитать, и заказчики требуют. Потому договорились рассчитывать так называемую лёдопроходимость (hл), т.е. толщину идеального сплошного ровного льда прочностью 500 кПа без снежного покрова, который может преодолеть судно, двигаясь на минимальной скорости ровным устойчивым ходом. Не строго, но хоть что-то, и позволяет сравнивать различные суда и ледоколы. Ледороходимость определяют сначала в ледовом бассейне. Большие учёные научились моделировать эту непредсказуемую среду, клацая зубами от холода и засеивая поверхность воды концентраторами кристаллообразования. Затем лёдопроходимость со всякими премудростями определяют на естественном полигоне. При этом как ни странно, получают результаты, близкие к модельным. Но в проекте тоже хочется сосчитать эту самую ледопроходимость. Придумано множество многоэтажных формул сложной структуры, иные даже с интегрированием по длине ватерлинии, хотя известно, что линейные интегралы не берутся в чистом виде.
Но один русский учёный – корабел (не специалист по гидромеханике, а сермяжный проектировщик) с корейской фамилией предложил красивую и простую формулу hпр=
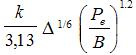, в которой k – коэффициент, определяемый по прототипу, Pe - тяга всех винтов т, и B - ширина судна по КВЛ в м, 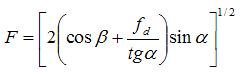- водоизмещение в т. Вот в этот прототип всё и уперлось. Судно, о котором сказано выше, имеет более острые обводы, чем все прототипы. Заказчик потребовал выполнить расчёт с учётом этого обстоятельства. В Hanze 97-го года выпуска, № 8 предложена функция, учитывающая влияние формы носовой оконечности на лёдопроходимость - , в которой α – угол входа ватерлинии на 1 – 2 теоретических шпангоутах, β - угол развала борта на тех же шпангоутах, fd – коэффициент динамического трения льда о корпус судна (в расчётах в первом приближении 0,1).После применения этой функции была получена формула hпр=
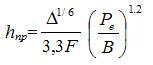.В ней тяга на винтах измеряется в кН. Коэффициент в знаменателе имеет слабую линейную зависимость от отношения ширины к осадке, но для расчётов можно оставить указанное в формуле значение.
